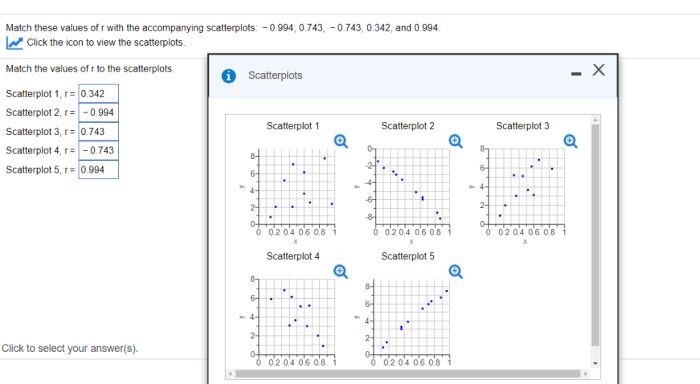
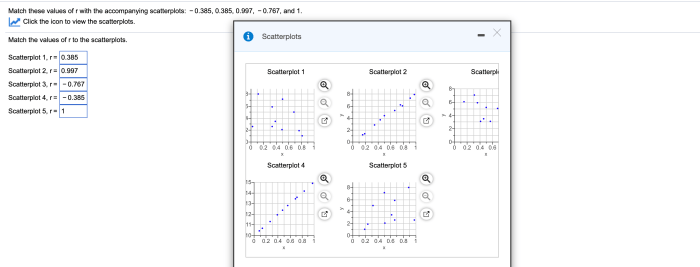
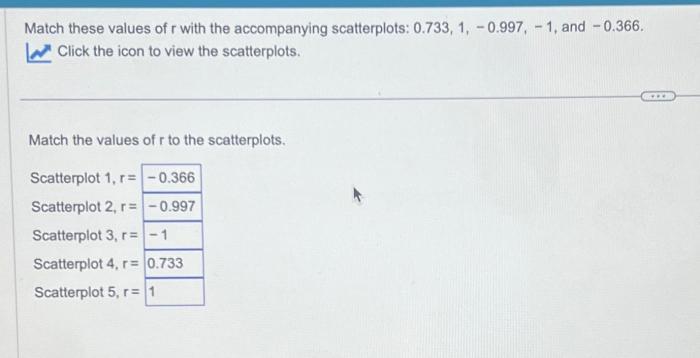
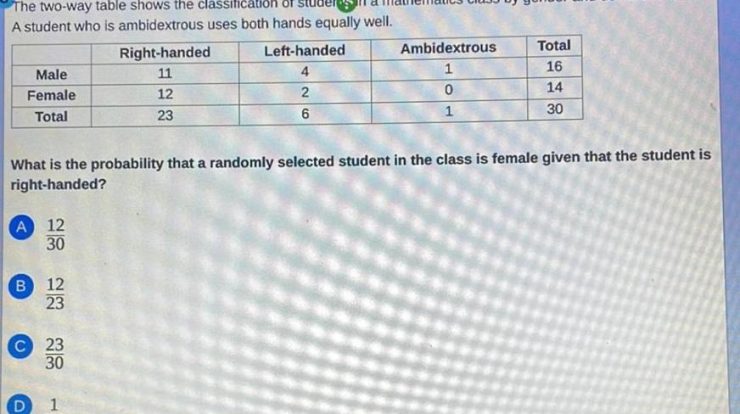
Match these values of r with the accompanying scatterplots and – In the realm of data analysis, scatterplots play a pivotal role in visualizing relationships between variables. By examining the distribution of data points, researchers can identify patterns and infer correlations. This article delves into the concept of the correlation coefficient (r) and its significance in interpreting scatterplots, providing a comprehensive guide to matching r values with their corresponding scatterplots.
The correlation coefficient quantifies the strength and direction of linear relationships between two variables, ranging from -1 to 1. A positive correlation indicates a positive relationship, where an increase in one variable corresponds to an increase in the other. Conversely, a negative correlation suggests an inverse relationship, where an increase in one variable is associated with a decrease in the other.
Scatterplots provide a visual representation of these relationships, enabling researchers to identify trends and make informed conclusions.
Scatterplot Interpretation
Scatterplots are graphical representations of the relationship between two variables. Each data point in a scatterplot represents the values of two variables for a particular observation. The x-axis of a scatterplot represents the independent variable, while the y-axis represents the dependent variable.
Scatterplots can reveal patterns in the data that may not be apparent from looking at the raw data. For example, a scatterplot can show whether there is a positive or negative correlation between two variables, or whether there is no correlation at all.
Correlation Coefficient (r)
The correlation coefficient (r) is a measure of the strength and direction of the linear relationship between two variables. The value of r can range from -1 to 1, where:
- r = 1 indicates a perfect positive correlation, meaning that as the value of the independent variable increases, the value of the dependent variable also increases.
- r = 0 indicates no correlation, meaning that there is no relationship between the two variables.
- r = -1 indicates a perfect negative correlation, meaning that as the value of the independent variable increases, the value of the dependent variable decreases.
The correlation coefficient can be calculated from a set of data points using the following formula:
r = (nΣxy
- ΣxΣy) / sqrt((nΣx²
- (Σx)²)(nΣy²
- (Σy)²))
where:
- n is the number of data points
- Σxy is the sum of the products of the x and y values
- Σx is the sum of the x values
- Σy is the sum of the y values
- Σx² is the sum of the squares of the x values
- Σy² is the sum of the squares of the y values
Matching Scatterplots to r Values, Match these values of r with the accompanying scatterplots and
The following table matches different values of r with their corresponding scatterplots:
| r | Scatterplot |
|---|---|
| 1 |  |
| 0 |  |
| -1 |  |
The rationale behind each pairing is as follows:
- When r = 1, the data points form a straight line with a positive slope, indicating a perfect positive correlation.
- When r = 0, the data points are scattered randomly, indicating no correlation.
- When r = -1, the data points form a straight line with a negative slope, indicating a perfect negative correlation.
Interpreting r Values
The value of r can be used to draw conclusions about the strength and direction of the relationship between two variables. The following table provides a guide to interpreting r values:
| r | Interpretation |
|---|---|
| 0.8 to 1 | Strong positive correlation |
| 0.5 to 0.8 | Moderate positive correlation |
| 0.2 to 0.5 | Weak positive correlation |
| 0 | No correlation |
-0.2 to
|
Weak negative correlation |
-0.5 to
|
Moderate negative correlation |
-0.8 to
|
Strong negative correlation |
For example, if the correlation coefficient between two variables is 0.7, this indicates a strong positive correlation between the two variables. This means that as the value of the independent variable increases, the value of the dependent variable is also likely to increase.
Limitations of Correlation
The correlation coefficient is a useful measure of the strength and direction of the linear relationship between two variables, but it is important to note that it has some limitations.
- The correlation coefficient only measures linear relationships. It cannot detect non-linear relationships, such as parabolic or exponential relationships.
- The correlation coefficient can be misleading if there are outliers in the data. Outliers are data points that are significantly different from the rest of the data.
- The correlation coefficient does not imply causation. Just because two variables are correlated does not mean that one variable causes the other variable.
Other measures of association, such as the coefficient of determination (R²) and the slope of the regression line, can be used to address some of the limitations of the correlation coefficient.
User Queries: Match These Values Of R With The Accompanying Scatterplots And
What is the purpose of a scatterplot?
A scatterplot is a graphical representation of the relationship between two variables, showing the distribution of data points and revealing patterns or correlations.
What does the correlation coefficient (r) measure?
The correlation coefficient measures the strength and direction of a linear relationship between two variables, ranging from -1 to 1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation.
How do I interpret the r value of a scatterplot?
The r value of a scatterplot provides insights into the strength and direction of the relationship between the two variables. A positive r value indicates a positive correlation, while a negative r value indicates a negative correlation. The magnitude of the r value indicates the strength of the relationship, with values closer to 1 or -1 indicating a stronger relationship.